Answer:
One has to work 7 hours as a cashier and 15 hours as a swimming teacher.
Explanation:
Suppose you have a job teaching swimming lessons and get paid $8 an hour. Let this be represented by 's'
You also have a job as a cashier and get paid $10 an hour. Let this be represented by 'c'
Given is you cannot work more than 22 hours a week, so equation forms:
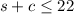
This becomes
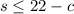
What are the number of hours you can work at each job and still make at least $190 is represented by :
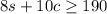
Putting values of 's' here,


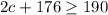
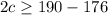

 hours
hours
So, s =
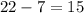 hours
hours
So, one has to work 7 hours as a cashier and 15 hours as a swimming teacher to make at least $190.