Answer:
The work done to move the object is 27 ft-lbs
B is correct.
Explanation:
A 4-lb. force acting in the direction of (4, -2).
First we find the unit vector of direction of force.
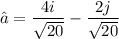
4-lb force acting in direction of vector a
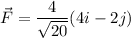
Object move 7 ft from point (0,4) to (5,-1)
Displacement vector whose length 7 ft
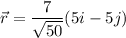
Now, we will find workdone by force
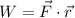
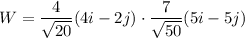
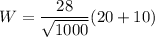
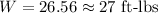
Hence, The work done to move the object is 27 ft-lbs