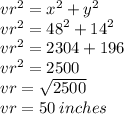Question

Two vectors, X and Y form a right angle. Vector X is 48 inches long and vector Y is 14 inches long. The length of the resultant vector is

Answer 1

First Photo - This is the problem drawn into the paper. If you have two vectors and they form a right angle (90°) between them, the Resultant Vector will appear like this, from the right angle.

Obs.:
1 - VR = Resultant Vector;
2 - The angle formed by the VR and the two vectors ISN'T a bisector.

Second Photo - You can move the bottom extremity of the Y vector to the arrow of the X vector and the tips from the Y and VR vectors will meet, forming a Right Triangle, whose the VR is the Hypotenuse (Opposes the right angle / Larger Side).

Now you just put the values in the Pythagorean Theorem:

`{a}^(2) = {b}^(2) + {c}^(2)`
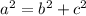
Where VR is the "a".


`{vr}^(2) = {x}^(2) + {y}^(2) \\ {vr}^(2) = {48}^(2) + {14}^(2) \\ {vr}^(2) = 2304 + 196 \\ {vr}^(2) = 2500 \\ vr = √(2500) \\ vr = 50 \: inches`