Answer:
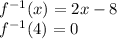
Explanation:
To find an inverse function, we need to think the function as an equality x = 1/2y + 4 that we have to resolve for the y.
First, let's subtract 4 from both sides.
x - 4 = 1/2y + 4 - 4
x - 4 = 1/2y
Now we multiply by 2 on both sides.
(x-4)*2 = 1/2y*2
2*x-8 = y
Therefore, the inverse function is
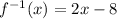
To find out
 , we need to replace the x of the function with a 4:
, we need to replace the x of the function with a 4:
 = 2*4 - 8 = 8 - 8 = 0
= 2*4 - 8 = 8 - 8 = 0
 = 0
= 0