Question

Given the geometric sequence where a1 = −3 and the common ratio is 9, what is the domain for n?

A) All integers
B) All integers where n ≥ −1
C) All integers where n ≥ 1
D) All integers where n ≥ 0

Answer 1

i think its B) All integers where n ≥ -1
i may be wrong

Answer 2

Option C - All integers , where
`n\geq 1`

Explanation:

Given : The geometric sequence where
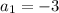`a_1 = -3` and the common ratio is 9,

To find : What is the domain for n?

Solution :

First we form a geometric sequence,

The nth term of geometric sequence is
`T_n=ar^(n-1)`

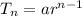
First term in GP,
`a_1 = -3`

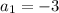
Common ratio, r = 9

Substitute the value,

`T_n=ar^(n-1)`

`T_n=(-3)(9)^(n-1)`

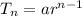
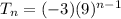
Now, what you get domain of
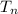`T_n` is all natural numbers e.g., n = {1, 2, 3, ......}

so, domain for n will be all integers where n ≥ 1

Hence, option (C) is correct.