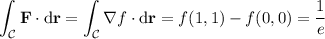If
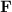
is conservative, then there is a scalar function

such that
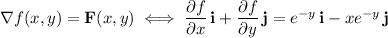
Setting the first components equal to one another, we can integrate both sides to find
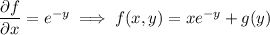
Differentiating both sides with respect to

gives
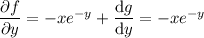
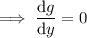

so that
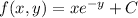
By the fundamental theorem of calculus, we have that