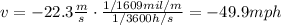Question

The railroad crossing lights turn red, so mckayla and her sister must stop and wait for the train to pass by. as they wait, mckayla's sister kylie grabs her phone and uses an app to measure the frequency of the approaching train's horn. the app reads 429 hz. assuming the train's original horn frequency is 400 hz and the speed of sound is 330 m/s, how fast is the train going in m/s and miles per hour

Answer 1

To calculate the speed of the train, you can use the formula for the Doppler effect. By plugging in the given values, you can find the speed of the train in m/s. To convert the speed to miles per hour, multiply by the conversion factor 2.237.

Step-by-step explanation:

The speed of the train can be calculated using the formula for the Doppler effect. The formula for calculating the observed frequency is given by:

fobs = fs * (v + vs) / (v + vo)

Where fobs is the observed frequency, fs is the source frequency, v is the speed of sound, vs is the velocity of the source towards the observer, and vo is the velocity of the observer towards the source. In this case, the source frequency is 400 Hz and the observed frequency is 429 Hz. By plugging in these values and solving for vs, you can find the speed of the train.

Once you have the speed of the train in m/s, you can convert it to miles per hour by multiplying by the conversion factor 2.237.

Answer 2

We can solve the problem by using the Doppler effect formula, which gives us the shift in frequency of a sound when the source is moving:

`f'= ( (v)/(v+v_s) ) f`
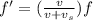
where
f' is the apparent frequency
v is the velocity of the wave

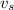
`v_s` is the velocity of the source relative to the observer
f is the original frequency

In our problem, f=400 Hz is the original frequency of the train's horn, f'=429 Hz is the apparent frequency read by the app, and v=330 m/s is the velocity of the wave (the speed of sound). If we re-arrange the formula, we can calculate v, the speed of the train:

`v_s = v ( (f)/(f')-1 )=(330 m/s)( (400 Hz)/(429 Hz)-1 )=-22.3 m/s`
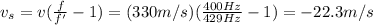
where the negative sign means the train is moving toward the two children.

In miles per hour, the velocity of the train is:

`v=-22.3 (m)/(s) \cdot (1/1609 mil/m)/(1/3600 h/s)= -49.9 mph`