The pressure exerted by the water at a depth of h=8513 m below the surface is given by Stevin's law:
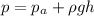
where
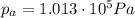
is the atmospheric pressure

is the water density

is the gravitational acceleration
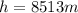
is the depth
If we plug the numbers into the formula, we find the pressure exerted on the window of the vehicle:
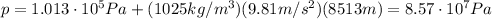
The area of the window is
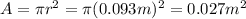
And so the force exerted on the window is
