Mean of the distribution = u = 222
Standard Deviation = s = 16
We have to find the probability that a value lies between 190 and 230.
First we need to convert these data values to z score.

For x = 190,
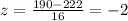
For x = 230
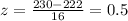
So, we have to find the percentage of values lying between z score of -2 and 0.5
P( -2 < z < 0.5) = P(0.5) - P(-2)
From standard z table, we can find and use these values.
P(-2 < x < 0.5 ) = 0.6915 - 0.0228 = 0.6687
Thus, there is 0.6887 probability that the data value will lie between 190 and 230 for the given distribution.