Answer:
The trignometric function which represents the graph is:
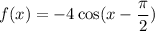
Explanation:
Based on the graph that is provided to us we observe that when
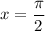
the value of the function is: -4
Hence, we will check which options holds true.
a)
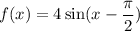
when
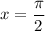 we have:
we have:
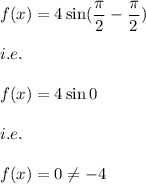
b)
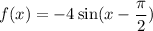
when
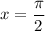 we have:
we have:
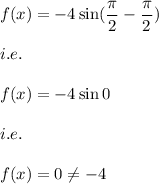
c)
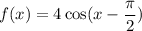
when
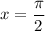 we have:
we have:
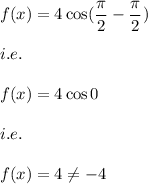
d)
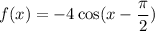
when
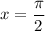 we have:
we have:
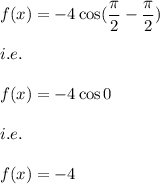
Also, when we plot the other points we observe that all the value satisfy the value as is given in the graph.
Hence, the graph of this function satisfies the given graph.