Question

Express the series using sigma notation. 6 + 9 + 12 + 15.

Answer 1

Each successive term differs from the prior term by 3, so we could write


`6=6+3(1-1)`

`9=6+3(2-1)`

`12=6+3(3-1)`

`15=6+3(4-1)`

Capturing this with sigma notation, we would set the changing value on each right hand side to the index variable,
`i`, which varies from 1 to 4. The sum is then given by


`\displaystyle\sum_(i=1)^4(6+3(i-1))`

Answer 2

The answer is
`\displaystyle\sum_(i=2)^53n`

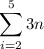
Explanation:

We can see that the numbers 6, 9,12 and 15 are multiples of 3 so if we multiple 3x2= 6, 3x3=9, 3x4= 12 and 3x5=5. We can see the 3 is in all the operations.

so we can create "the formula for the terms." that will be 3n where n is the variable which would change as marked. In the top of the Σ would be the last value of n and on the bot would be the first number.

with the operations showed before we can see that the first value of n is 2 and the last number is 5.

with this now we can resolve the question:

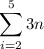`\displaystyle\sum_(i=2)^53n`= 3(2)+3(3)+3(4)+3(5)

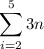`\displaystyle\sum_(i=2)^53n`= 6+9+12+15