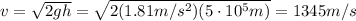Question

Io, a satellite of Jupiter, has volcanoes that send plumes of matter over 500 km high. The acceleration due to gravity on Io is only 1.81 m/s2, and Io has no appreciable atmosphere. Assuming that there is no variation in gravity over the distance traveled, what must be the speed of the material just as it leaves the volcano in order to reach an altitude of 500 km?

Answer 1

We can solve the problem by using the conservation of energy.

In fact, in order to reach an altitude of h above the ground, the initial kinetic energy of the material must be equal to the final gravitational potential energy at altitude h:

`(1)/(2)mv^2 = mgh`
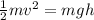
where the term on the left is the kinetic energy, and the term on the left is the gravitational potential energy, and where
m is the mass of the material
v is its initial velocity
g is the gravitational acceleration on Io
h is the altitude

If we use the data of the problem:

`h=500 km = 5 \cdot 10^5 m`

`g=1.81 m/s^2`
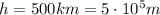
And we re-arrange the formula, we find the velocity the material should have in order to reach the altitude of 500 km:

`v= √(2gh) = √(2(1.81 m/s^2)(5 \cdot 10^5 m)) =1345 m/s`