Question

Select the graph that would represent the best presentation of the solution set. |1 - 4x| > 7

Answer 1

here's the answer

Explanation:

Answer 2

Hi, the set of graph choices is missing. Nevertheless, I can solve the inequality, find the soluction set and graph it.

Remember the definition of the absolute value function:


`|x|= \left \{ {{x,{ifx\ \textgreater \ 0} \atop {-x},ifx\ \textless \ 0} \right.`

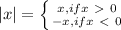
So, to solve |1-4x|>7, you have to considerer two cases:

1) Case 1: If 1 - 4x > 0, the solution is:

1 - 4x > 7

Which you solve in this way:

subtract 1 in both sides ⇒ -4x > 6
divide by - 4 ⇒ x < -6/4
simplify the fraction x < -3/2

2) Case 2: If 1 - 4x < 0, the solution is:

1 - 4x < - 7 ⇒

subtract -1: - 4x < - 8
divide by - 4: x > 8/4
simplify the fraction: x > 2

Therefore the solution is (-∞, -3/2) ∪ (2,∞), whose graph is the one attached.