Question

If the beam cuts the water spray at points A and B, such that point B is at a higher level than point A, what distance from the ground level is point A?

1.66 units


4.15 units


5.44 units


6.14 units


7.13 units

Answer 1

Answer: option B. 4.15 units

Step-by-step explanation:

Hi. The statement is incomplete.

This is the complete statement:

A fountain on a lake sprays water in a parabolic arch modeled by the equation y = -0.3x² + 3x. A beam of light modeled by the equation
-2x + 5.5y = 19.5 passes through the fountain to create a rainbow effect. If the beam cuts the water spray at points A and B, such that point B is at a higher level than point A, what distance from the ground level is point A?
A) 1.66 units
B) 4.15 units
C) 5.44 units
D) 6.14 units
E) 7.13 units

To solve that problem you must find the solution of the system of the equations defined by the two given equations:


`\left \{ {{y=-0.3 x^(2) +3x} \atop {-2x+5.5y=19.5}} \right`

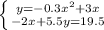
Thi is the solution of the system:

i) replace y from the first equation into the second equation:

-2x + 5.5 [-0.3x² + 3x] = 19.5

ii) distributive property: -2x - 1.65x² + 16.5x = 19.5

iii) comine like terms: - 1.65x² + 14.5x = 19.5

iv) transpose terms: 1.65x² - 14.5x + 19.5 = 0

v) use quadratic formula to find the solution: they are x ≈ 1.66 and x ≈ 7.13.

To find which is the lower point, you replace the two values and find which has smaller y value:

y = -0.3x² + 3x

x = 1.66 ⇒ y = -0.3(1.66)² + 3(1.66) = 4.15

x = 7.13 ⇒ y = -0.3(7.13)² + 3(7.13) = 6.14

Therefore, the answer is y = 4.15, which is the option B.