Question

A contractor buys 16 yd of nylon carpet and 22 yd of wool carpet for $1902. A second purchase, at the same prices, includes 20 yd of nylon carpet and 21 yd of wool carpet for $2033. Find the cost per yard of the wool carpet.

Answer 1

$53

Explanation:

Given that, two type of clothes nylon and wool carpet.

Let the price of one yard of nylon carpet = $
`x`

Let the price of one yard of wool carpet = $
`y`

Price for 16 yd of nylon carpet and 22 yd of wool carpet = $1902

Price for 20 yd of nylon carpet and 21 yd of wool carpet = $2033

Writing equations as per given statement:

`16x+22y=1902 ...... (1)\\20x+21y=2033 ...... (2)`

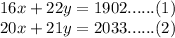
Here, we have to find the value of
`y`.

By equation (1), we get:

`16x = 1902 - 22y \\\Rightarrow x = (1)/(16)(1902-22y) ..... (3)`

Putting the value from equation (3) to equation (2):

`20 ((1)/(16)(1902-22y) ) + 21y =2033\\\Rightarrow 9510-110y + 84y = 8132\\\Rightarrow 26y=1378\\\Rightarrow \bold{y = 53}`

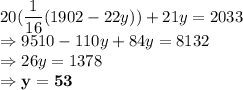
Therefore, the cost per yard for the wool carpet is $53.