Question

Let f(x) = x^2 + 6 and g(x) = x+8/x . Find ( g o f)(­ -7)

Answer 1

One way to approach this is to find (g o f)(x) first and then to replace x by -7:

g( f(x) ) = (x^2+6) + 8/(x^2+6)

Now replace x with -7. We get: ( g o f )(-7) = 49+6+8 / (49+6), or
= 55 + 8 / 55, or 55 8/55 (ans.)

Answer 2

Answer:

`(63)/(55)`

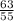Step-by-step explanation:
(g o f)(-7) is a composite function.
It means that we are going to substitute each x in the g function with f(x) and then substitute in the final expression with x = -7

Therefore, we will do this on two steps as follows:
1- getting (g o f)(x):
we have:
f (x) = x² + 6
g (x) =
`(x+8)/(x)`

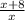
Therefore:
(g o f)(x) =
`(x^2+6+8)/(x^2+6) = (x^2+14)/(x^2+6)`

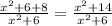2- getting (g o f)(-7):
We will simply substitute with x = -7 in the expression obtained from part 1 as follows:
(g o f)(x) =
`(x^2+14)/(x^2+6)`

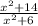
(g o f)(x) =
`((-7)^2+14)/((-7)^2+6)` =
`(63)/(55)`

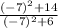
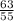
Hope this helps :)