The
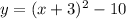 is the quadratic equation in the desired form.
is the quadratic equation in the desired form.
The
 is the quadratic equation in the desired form.
is the quadratic equation in the desired form.
a)
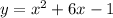 :
:
To rewrite this quadratic equation in the form
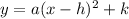 , we complete the square:
, we complete the square:
![\[ y = x^2 + 6x - 1 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/h51knxkvgxhx4540si9elknxpdruflh5i7.png)
1. **Group the x-terms:**
![\[ y = (x^2 + 6x) - 1 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zmzz3y6g1vznvjg5t9dpzwd7s049oepc9c.png)
2. **Complete the square (add and subtract
 :**
:**
![\[ y = (x^2 + 6x + 9 - 9) - 1 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/275ql571ixw4jg9tbuxjtlnm61haf5085n.png)
3. **Factor the perfect square trinomial and simplify:**
![\[ y = (x + 3)^2 - 10 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/vjlwk4g3kvjuaam0znav4xu17iamv1rpht.png)
So,
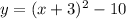 is the quadratic equation in the desired form.
is the quadratic equation in the desired form.
b.
 :
:
To rewrite this quadratic equation in the form
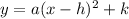 , we complete the square:
, we complete the square:
![\[ y = x^2 - 6x - 4 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/jbd40fj42j0k49c3fxyl1bpfwalranssqm.png)
1. **Group the x-terms:**
![\[ y = (x^2 - 6x) - 4 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zpn645g35e3py5rbbya8i59pjedj8p2rfd.png)
2. **Complete the square (add and subtract
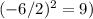 :**
:**
![\[ y = (x^2 - 6x + 9 - 9) - 4 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/a7rr038e6mo98ixto10fs0yu3eld9e3mgx.png)
3. **Factor the perfect square trinomial and simplify:**
![\[ y = (x - 3)^2 - 13 \]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zqci6dd1nfycf3f423g1qbirgivveb1pyp.png)
So,
 is the quadratic equation in the desired form.
is the quadratic equation in the desired form.