Answer:
Option 4
Explanation:
Given : Geometric sequence
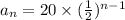
To find : Which spreadsheet would be used to compute the first 7 terms of the geometric sequence ?
Solution :
Geometric sequence is in the form
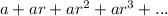
Where, a is the first term and r is the common ratio.
The sum of sequence is represented as
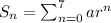
or
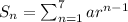
According to question,
a=20 and
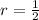
Sum of first terms is,
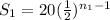 ,
,
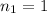
Sum of second terms is,
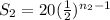 ,
,
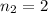
Sum of third terms is,
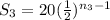 ,
,
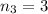
Sum of four terms is,
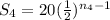 ,
,
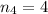
Sum of five terms is,
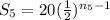 ,
,
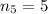
Sum of six terms is,
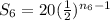 ,
,
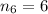
Sum of seven terms is,
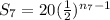 ,
,
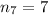
Therefore, Option 4 is correct.
The spreadsheet 4 would be used to compute the first 7 terms of the geometric sequence.