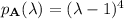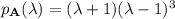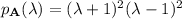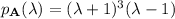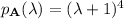Question

A 4x4 matrix a with real entries and a4 = i, what are the possible characteristic polynomials of a

Answer 1

If
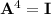
`\mathbf A^4=\mathbf I`, then the characteristic polynomial of
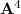
`\mathbf A^4` is


`p_(\mathbf A^4)(\lambda)=\det(\lambda\mathbf I-\mathbf A^4)=\det((\lambda-1)\mathbf I)=(\lambda-1)^4`

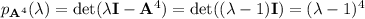
which means
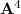
`\mathbf A^4` has eigenvalues
`\lambda=1`.


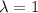
We know that if
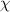
`\chi` is an eigenvalue of
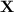
`\mathbf X`, then
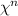
`\chi^n` is an eigenvalues of
`\mathbf X^n`.


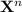
So if
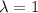
`\lambda=1` is the only eigenvalue of
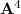
`\mathbf A^4`, we know that
`\pm\sqrt[4]\lambda=\pm1` are the only possible eigenvalues of
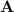
`\mathbf A`. We can construct five possible characteristic polynomials for
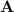
`\mathbf A` in that case.


`p_(\mathbf A)(\lambda)=(\lambda-1)^4`

`p_(\mathbf A)(\lambda)=(\lambda+1)(\lambda-1)^3`

`p_(\mathbf A)(\lambda)=(\lambda+1)^2(\lambda-1)^2`

`p_(\mathbf A)(\lambda)=(\lambda+1)^3(\lambda-1)`

`p_(\mathbf A)(\lambda)=(\lambda+1)^4`