Question

Consider rectangle pqrs with pq=10 and ps=24. if a and b are the midpoints of sides pq nd qr respectively,find ab

Answer 1

The midpoint of side pq is 5 and since qr is parallel to ps the midpoint of qr is 12.

Answer 2

Hence, ab=13

Explanation:

" Mid-point is a point which divide the line segment into two equal parts that is the dimension of both the parts on the left and right of that point are equal "

Now as we are given a rectangle pqrs such that pq=10 and ps=24.

also a and b are the midpoints of sides pq and qr respectively.

as pqrs is a rectangle.

Hence, pq=rs and ps=qr

Hence, qr=24 units.

Now as a is mid point of pq.

Hence, length of pa=5 units (since 10/2=5)

and aq=5 units (since 10/2=5).

similarly qb=12 (since 24/2=12)

br=12 (since 24/2=12)

Now ab could be find out by forming a right angled triangle as measure of each of the angles of a rectangle are 90°.

Hence we will consider a right angled triangle as aqb.

As aq=5, qb=12 ,

now using the Pythagorean theorem we have:

`ab^2=aq^2+qb^2\\\\ab^2=5^2+12^2\\\\ab^2=25+144=169=13^2\\\\ab=13`

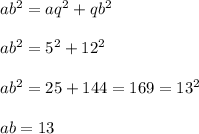
Hence, ab=13