Answer:
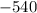
Explanation:
From binomial theorem, we can know
first term would be x^6
2nd term x^5
3rd term x^4
4th term x^3
Also, from binomial theorem, we can know
first term would be y^0
2nd term would be y^1
3rd term would be y^2
4th term would be y^3
We can see that we are looking for the 4th term (x^3y^3).
To find coefficient of 4th term, we use write:
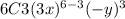
We can expand 6C3 using formula:

Now, we have:
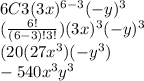
Thus, the coefficient is -540