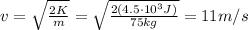Question

A 1.2-mol sample of hydrogen gas has a temperature of 21 ∘C.

Part A
What is the total translational kinetic energy of all the gas molecules in the sample?
Express your answer using two significant figures.


K =

5
J
Previous AnswersRequest Answer
Incorrect; Try Again; 4 attempts remaining
Part B
How fast would a 75-kg person have to run to have the same kinetic energy?
Express your answer using two significant figures.


v =

m/s

Answer 1

A) The average translational kinetic energy of the molecules in a gas is given by:

`K = (3)/(2)k_B T`
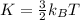
where

`k_B` is the Boltzmann's constant
T is the absolute temperature of the gas

In our problem,
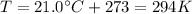
`T=21.0^(\circ)C +273 = 294 K`, so the average translational kinetic energy of the molecules is

`K= (3)/(2)(1.38 \cdot 10^(-23) J/K)(294 K)=6.09 \cdot 10^(-21) J`

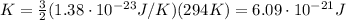
We have 1.2 mol of this gas, and since one mole of ideal gas contains a number of molecules equal to Avogadro number, the total number of molecules in our gas is

`N=n N_A = (1.2 mol)(6.022 \cdot 10^(23) mol^(-1) ) =7.35 \cdot 10^(23)`

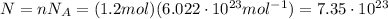
So the total translational kinetic energy of all molecules of the gas is

`K_(tot)= NK = (7.35 \cdot 10^(23))(6.09 \cdot 10^(21) J)=4476 J = 4.5 \cdot 10^3 J`


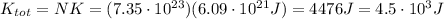
B) The kinetic energy of a person is given by:

`K= (1)/(2)mv^2`
where m is the person's mass and v his velocity. The person has a mass of m=75 kg and its energy is equal to the energy of the gas,
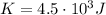
`K=4.5 \cdot 10^3 J`, therefore his velocity must be

`v= \sqrt{ (2K)/(m) }= \sqrt{ (2 (4.5 \cdot 10^3 J))/(75 kg) } =11 m/s`