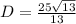Answer:
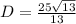
Explanation:
Given
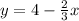
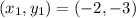
Required
Determine the distance
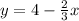
Write the above equation in standard form:
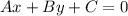
So, we have:
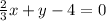
By comparison:

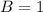 and
and
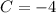
The distance is calculated using:
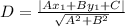
Where:
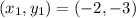

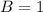 and
and
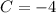
This gives:
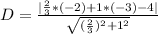
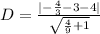
Take LCM
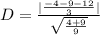

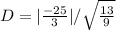
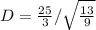
Split the square root
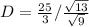
Change / to *
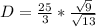
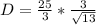
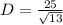
Rationalize
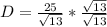
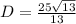
Hence, the distance is: