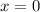For this case we must solve the following equation:
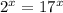
For this, we follow the steps below:
We find the Neperian logarithm on both sides of the equation to remove the variable from the exponent
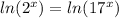
We use one of the logarithm properties to extract x from the exponent:
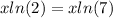
We subtract xln (7) on both sides of the equation:
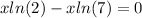
We take x common factor:
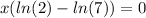
We divide between
 on both sides of the equation, then:
on both sides of the equation, then:
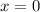
Answer: