Question

Find the area of the shaded regions. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answer 1

Answer: 40 pi

Explanation:

Answer 2

Hello!

The formula for the area of a sector can be written as follows:

Area =
`(1)/(2)`
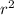
`r^(2)`(R)

In the above formula, “r” represents the radius while “R” represents the radian measure of a sector. The radius is given to us in the image above as 10 inches. However, we still need the radian measure of the two sectors. To find this measure, we can use the following conversion:

1 degree =
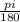
`(pi)/(180)` radians

Because the two sectors have a given measure of 72 degrees, we need to multiply both sides of the above conversion by 72:

72 degrees =
`(72pi)/(180)`

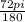
Reduce the fraction on the right side of the equation:

72 degrees =
`(2pi)/(5)`

We now have the radian measure of both sectors. Now simply insert this and any other known values into the “area of a sector” formula above:

Area =
`(1)/(2)`
`10^(2)`(
`(2pi)/(5)`)

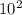
Simplify the right side of the equation to get the following answer:

Area = 20 pi

We have now proven that the area of one sector is equal to 20 pi.

If, however, you need the combined area of the two identical sectors, simply multiply the proven area by 2 to get a total area of 40 pi.

I hope this helps!