Question

A pyramid has a regular hexagonal base with side lengths of 4 and a slant height of 6. Find the total area of the pyramid.

T. A. =

Answer 1

Since this pyramid has a regular hexagonal base with side lengths of 4 and a slant height of 6, the total area of the pyramid is:

T.A =
`72+24√(3)` square units.

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

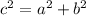
Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

Note: The radius (r) of the pyramid is equal to the side length.

In order to determine the total area (T.A) of this pyramid, we would have to find its apothem (a) by applying Pythagorean's theorem;

`a^2 = 4^2 - 2^2\\\\a^2 = 16-4\\\\a=√(12) \\\\a=2√(3) \;units`

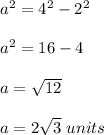
The total area (T.A) of this pyramid can be calculated by using this formula;

T.A = 3bs + 3ab

where:

• a is the apothem.
• b is the side length.
• s is the slant height.

By substituting the parameters, we have;

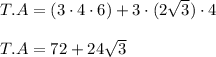`T.A = (3 \cdot 4 \cdot 6) + 3 \cdot (2√(3) ) \cdot 4\\\\T.A =72+24√(3)`square units.

Answer 2

The area is given by:
A = Ab + Al
Where,
Ab: base area
Al: lateral area
The area of the base is:
Ab = (3/2) * (L ^ 2) * (root (3))
Where,
L: side of the hexagon.
Substituting we have:
Ab = (3/2) * (4 ^ 2) * (root (3))
Ab = (3/2) * (16) * (root (3))
Ab = 24raiz (3)
The lateral area is:
Al = (6) * (1/2) * (b) * (h)
Where,
b: base of the triangle
h: height of the triangle
Substituting we have:
Al = (6) * (1/2) * (4) * (6)
Al = 72
The total area is:
A = 24raiz (3) + 72
Answer:
A = 24raiz (3) + 72