Question

Find the height of the triangle

Answer 1

The given triangle is a right angle. To solve this, we can use;

sin theta = opposite / hypotenuse ; where theta =20 ; h = 10
sin (20) = x / 10
x = 3.42

The answer is the fourth one, 3.42

Answer 2

There are two -main- approaches to answer this problem. By using the sine identity, or applying law of sines.

We'll do the sine trig. identity, as it is the most effective.

Given an angle '
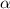
`\alpha`' in a right triangle, '
`sin( \alpha )`' is defined as the opposite side of the triangle to the given angle, over the triangle's hypotenuse.

So, for this setup:

`sin(20)= (x)/(10)`

Now, we solve for x:

`x=10sin(20)=3.42`

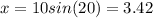So, answer is 3.4