Question

For the arithmetic sequence beginning with the terms {5, 6, 7, 8, 9, 10...}, what is the sum of the first 17 terms

Answer 1

Answer: S = 221

Explanation: An arithmetic sequence is a set of numbers in order, having the difference between one term and the next a constant.

The sum of an arithmetic sequence can be calculated as the following formula:

`S=(n)/(2) [2a_(1)+(n-1)r]`

where

n is how many terms to add

a₁ is the 1st term of the sequence

r is the constant

For the sequence above:

`S=(17)/(2) [2(5)+(17-1)1]`

`S=(17)/(2)(26)`

`S=17(13)`

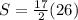
S = 221

The sum of the first 17 terms of the arithmetic sequence {5,6,7,8,9,10...} is 221