Question

Find the lateral area the regular pyramid.

Answer 1

180

Explanation:

The general formula for the lateral surface area of a regular pyramid is

L.S.A = 1/2 (p)(l)

where p represents the perimeter of the base and l the slant height

Slant height

The hexagon can be broken down into 6 equilateral triangles. Each side of the equilateral triangle is equal, therefore, the diagonal is twice the side length of the hexagon and the distance from one vertex to mid is half the diagonal.

By considering a right triangle at the centre, we will apply pythagorus theorem

Hypotenuse² = base² + height²

slantHeight² = 6² + 8²

slantHeight = √(6²+8²)

= 10

Perimeter of base

6(6) = 36

L.S.A = 1/2 (36)(10)

= 180

Answer 2

The lateral area of the pyramid is 180 unit².

Explanation:

We are given a hexagonal pyramid with dimensions,

Base (B)= 6 units and Height (H) = 8 units

Now, the lateral area of the pyramid =
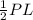`(1)/(2)PL`, where P = perimeter of the base and L = slant height.

Since, the base of the pyramid is a hexagon.

So, the perimeter of an hexagon =
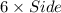`6* Side` = 6 × 6 = 36 units

Also, the slant height is given by,

`L^(2)=\sqrt{B^(2)+H^(2)}\\\\L^(2)=\sqrt{6^(2)+8^(2)}\\\\L^(2)=√(36+64)\\\\L^(2)=√(100)\\\\L=\pm 10`

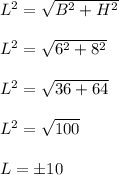
Since, the slant height cannot be negative. So, L = 10 units.

Substituting the values gives,

The lateral area of the pyramid =
`(1)/(2)* 36* 10=36* 5=180`

Thus, the lateral area of the pyramid is 180 unit².