Solution:
we are given that ΔABC and ΔXYZ are similar triangles.
As we know , when two triangles are similar then the ratios of their corrsponding sides are equal.
Here we have
BA = x + 9, AC = x + 7, YX = x + 5, and XZ = x + 4
So we can write
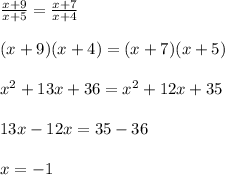
Hence then value of x=-1.