Question

Two students in different classes took the same math test. Both students received a score of 87. In student A's class the mean was 78 and the standard deviation of 5. In student B's class the mean was 76 with a standard deviation of 4. Which student scored in the top 10% of their class?

A. student b
b. student a
C. both students
D. neither student

Answer 1

Answer: Student B will score in the top of the class.

Explanation:

Here both the students of class A and B scored 87.

Therefore, the value of random variable for both class is, x = 87

According to the question, mean for the class A is,
`\mu_1 = 78`

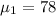
And, standard deviation for class A,
`\sigma_1 = 5`

Thus, the z-score for Class A,

`z_1 = (x-\mu_1)/(\sigma_1)`

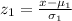
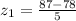`z_1 = (87-78)/(5)` = 9/5 = 1.8

And,
`z_1(1.8)=0.9641`

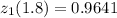
Also, mean for the class B is,
`\mu_2 = 76`

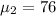
And, standard deviation for class B,
`\sigma_2 = 4`

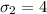
Thus, the z-score for Class B,

`z_2 = (x-\mu_2)/(\sigma_2)`

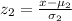
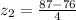`z_2 = (87-76)/(4)` = 11/4 = 2.75

`z_2(2.75)=0.9970`

Thus,
`z_2 > z_1`

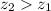
Therefore, student B scored in the top 10% of their class.