Question

(08.02 MC) A grain silo is shown below: Grain silo formed by cylinder with radius 6 feet and height 168 feet and a half sphere on the top What is the volume of grain that could completely fill this silo, rounded to the nearest whole number? Use 22 over 7 for pi.

Answer 1

Hello!!!!

Find the volume of the bottom and top separately and then add them. Cylinder volume is the area of the bottom times the height (22/7)(5^2)•175=13750 ft^3
The volume of a sphere isV=(4/3)(22/7)r^3where r is the radius. Here that's also 5 since it fits on the cylinder. Also we only want half the sphere so useV=(2/3)(22/7)•5^3=261.9 ft^3Which we round upto 262. Now add the parts together 13750+262=14,012 ft^3
Hope this helps!

Answer 2

19460 cubic feet

Explanation:

Since we are given that Grain silo is formed by cylinder and a half sphere on top

We are required to find the volume of grain that could completely fill this silo

Formula of volume of cylinder :
`\pi r^(2)h`

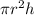
Since we are given that the cylinder with which the silo is formed has height 168 feet and radius 6 feet

So, r = 6 feet

h = 168 feet

use π =22/7

Substituting these values in formula

Volume of cylinder
`= (22)/(7)*(6)^(2) * 168`

`= (22)/(7)*36* 168`

`= 19008 feet^(3)`

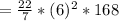
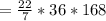
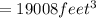
Thus the volume of cylinder is 19008 cubic feet.

Now since the silo is fomed of half sphere also

Formula of volume of sphere
`=(4)/(3) \pi r^(3)`

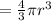
Volume of half sphere
`=((4)/(3))/(2) \pi r^(3)`

`=(2)/(3) \pi r^(3)`

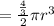
Since r = 6 feet

So, volume of half sphere
`=(2)/(3) * (22)/(7)*(6)^(3)`

`=452.57`

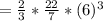
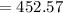
Thus the volume of half sphere is 452.57 cubic feet.

Thus the volume of the grain = volume of cylinder +volume of half sphere

=19008+452.57

=19460.57 cubic feet

Hence the volume of grain that could completely fill this silo is 19460 cubic feet ( rounded to the nearest whole number )