Answer : The correct answer for amount of radioisotope remain in 2030 is 0.619 g .
Radioactive Decay is emission of radiations ( in form of alpha , beta particle etc ) by unstable atom .
Radioactive decay is FIRST ORDER reaction . So , the equation of first order can be used to find decay constant , amount of radioisotopes or half life .
The equation for radioactive decay is given as :
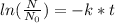
Where : N = amount of radioisotope at time t
N₀ = amount of radioisotope initially present
k = decay constant t = time
Half life :
It is time when amount of radioisotope decrease to 50 % of its original amount . Half life
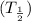 and decay constant can be related :
and decay constant can be related :
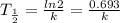
Following are the steps can be used to determine amount of radioisotope (N) :
1) To find decay constant :
Given :
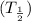 = 28 yrs
= 28 yrs
Decay constant can be calculated using half life by plugging value in half life formula :

On multiplying both side by k
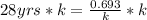
On dividing both side by 28 yrs
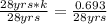
k = 0.02475 yrs⁻¹
2) To find amount of radioisotope (N):
Given : Amount of radioisotope originally present = 3.5 g
Time = 2030 - 1960 = 70 yrs
decay constant = 0.02475 yrs⁻¹
Amount of radioisotope (N) = ?
Plugging these values in the formula as:


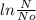 can be converted using the formula (
can be converted using the formula (
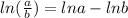 )
)
ln N - ln (3.5 ) = - 1.7325
(ln 3.5 = 1.253 )
ln N -1.253 = -1.7325
Adding both side 1.253
ln N -1.253 + 1.253 = -1.7325 + 1.253
ln N = -0.4795
Taking anti ln of -0.4795
N = 0.619 g
Hence amount of radioisotope remained in 2030 is 0.619 g