Question

Which equation is the perpendicular bisector of the line segment with endpoints (-2,4) (6,8)

Answer 1

Answer:
y = -2x + 10

Step-by-step explanation:
The general equation of the linear line is:
y = mx + c
where m is the slope and c is the y-intercept

1- getting the slope:
slope of the given two points is:
slope =
`(8-4)/(6--2) = 1/2`

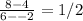
We know that the line we are looking for is perpendicular to the line having these two points. Therefore, the product of the slope should be equal to -1.
This means that the slope of the line we are looking for is -2
The equation of the line we are looking for now is:
y = -2x + c

2- getting the y-intercept:
To get the y-intercept, we need a point that belongs to the line.
We know that the line passes through the midpoint of (-2,4) and (6,8). Therefore, we need to get the midpoint first:
midpoint = (
`(x1+x2)/(2) , (y1+y2)/(2)`)

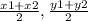
midpoint = (2,6)
Now, to get the value of the c, we will use the point we have, substitute in the equation and solve for c as follows:
y = -2x + c
6 = -2(2) + c
6 = -4 + c
c = 10

Based on the above, the equation of the line is:
y = -2x + 10

Hope this helps :)