Answer: The correct option is (A) 42.7 units.
Step-by-step explanation: Given that the radius of the circle center at O is 24 units and OC is 11 units.
We are to find the length of chord AB.
We have,
in the right-angled triangle OCB (m∠OCB = 90°),
OB = 24 units and OC = 11 units.
Using Pythagoras theorem in ΔOCB, we have
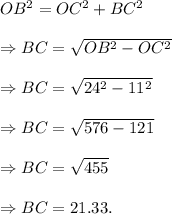
Since OC is perpendicular to chord AB, so AC = BC.
Therefore, we get
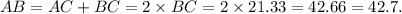
Thus, the required length of AB is 42.7 units.
Option (A) is CORRECT.