Question

These tables of values represent continuous functions. In which table do the values represent an exponential function?

A.
x y
1 3
2 6
3 9
4 12
5 15
B.
x y
1 2
2 6
3 18
4 54
5 162
C.
x y
1 10
2 22
3 34
4 46
5 58
D.
x y
1 7
2 8
3 9
4 10
5 11

Answer 1

Table B represents an exponential function.

Explanation:

An exponential function is a function which has common ratio. Using this fact we will evaluate the functions given in the form of a table.

Table A.

f(1) = 3

f(2) = 6

f(3) = 9

Now
`(f(2))/(f(1))=(6)/(3)=(2)/(1)`

`(f(3))/(f(2))=(9)/(6)=(3)/(2)`

Ratios are not equal so it's not an exponential function.

Table B.

f(1) = 2

f(2) = 6

f(3) = 18

`(f(2))/(f(1))=(6)/(2)=(3)/(1)`

`(f(3))/(f(2))=(18)/(6)=(3)/(1)`

Here ratios are same therefore it's an exponential function.

Table C.

f(1) = 10

f(2) = 22

f(3) = 34

`(f(2))/(f(1))=(22)/(10)=(11)/(5)`

`(f(3))/(f(2))=(34)/(22)=(17)/(11)`

Ratios are not equal therefore it's not an exponential function.

Table D.

f(1) = 7

f(2) = 8

f(3) = 9

`(f(2))/(f(1))=(8)/(7)`

`(f(3))/(f(2))=(9)/(8)`

Ratios are not equal so it's not an exponential function.

Therefore Table B is the correct option.

Answer 2

The correct option is B.

Explanation:

A function is called an exponential function if it has common ratio.

A function is called an linear function if it has common difference.

In option A.

`(f(2))/(f(1))=(6)/(3)=2`

`(f(3))/(f(2))=(9)/(6)=(3)/(2)`

`2\\eq (3)/(2)`

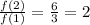
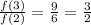
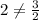
Since the given table has different ratio, therefore it is not an exponential function. Option A is incorrect.

In option B.

`(f(2))/(f(1))=(6)/(2)=3`

`(f(3))/(f(2))=(18)/(6)=3`

`3=3`

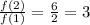
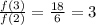
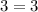
Since the given table has common ratio, therefore it is an exponential function. Option B is correct.

In option C.

`(f(2))/(f(1))=(22)/(10)=(11)/(5)`

`(f(3))/(f(2))=(34)/(22)=(17)/(11)`

`(11)/(5)\\eq (17)/(11)`

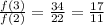
Since the given table has different ratio, therefore it is not an exponential function. Option C is incorrect.

In option D.

`(f(2))/(f(1))=(8)/(7)`

`(f(3))/(f(2))=(9)/(8)`

`(8)/(7)\\eq (9)/(8)`

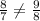
Since the given table has different ratio, therefore it is not an exponential function. Option D is incorrect.