Question

The equation of the model is: d = 6cos(πt) Graph the function using the graphing calculator. Find the least positive value of t at which the pendulum is in the center. t = -0.5 sec To the nearest thousandth, find the position of the pendulum when t = 4.25 sec.

Answer 1

t=0.5sec
d=4.243in
just did it

Answer 2

We have been given a trigonometric function
`y=6cos(\pi t)`.

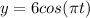The graph of this function has been graphed using a graphing calculator and it is attached below.

Our next step is to find the time when pendulum passes the center or equilibrium position for the first time. In order to figure this time out, we need to set y=0 and solve for time t.

`6cos(\pi t)=0\Rightarrow cos(\pi t)=0\Rightarrow \pi t=(\pi)/(2)\Rightarrow t=(1)/(2)`

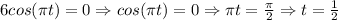
Therefore, the least positive value of t at which the pendulum is in the center is 0.5 seconds.

Next, we need to find the position of pendulum at time
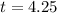`t=4.25` seconds.

In order to do so, we will substitute
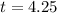`t=4.25` in the function
`y=6cos(\pi t)`.

`y=6cos(\pi\cdot 4.25)=6((1)/(√(2)))=3√(2)\approx 4.243`

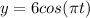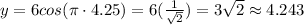
Therefore, position of pendulum is 4.243 units away from center.