Question

Can any kind soul help me ASAP!​

Answer 1

Answer:
`(-2p^2+10p-8)/(p^2-4)`

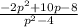
This can be written as (-2p^2+10p-8)/(p^2-4) on a keyboard.

=======================================================

Work Shown:

`(2p)/(p^2-4) + (4-2p)/(p+2)\\\\\\(2p)/((p+2)(p-2)) + (4-2p)/(p+2)\\\\\\(2p)/((p+2)(p-2)) + ((4-2p)(p-2))/((p+2)(p-2))\\\\\\(2p+(4-2p)(p-2))/((p+2)(p-2))\\\\\\(2p-2p^2+8p-8)/(p^2-4)\\\\\\(-2p^2+10p-8)/(p^2-4)\\\\\\`

---------------------

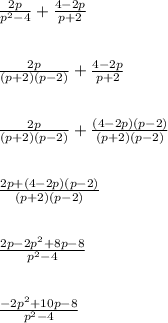
Explanations:

• In step 2, I factored p^2-4 using the difference of squares rule.
• In step 3, I multiplied top and bottom by (p-2) so that the second fraction has a denominator of (p+2)(p-2). We can only add fractions that have the same denominator.
• In step 5, I used the FOIL rule to expand (4-2p)(p-2) into -2p^2+10p-8. You can use the distribution rule or the box method as alternatives.