Question

How can operations of polynomials be used to create new polynomial models? Provide real world examples of when it is necessary to add, subtract, multiply, or compose polynomials to get a new polynomial that model real situations.

Answer 1

Answer with explanation:

When we add, subtract or multiply or in some cases division is done between two or more Polynomials then we can get new polynomials.

This can be explained in following way

`1.\rightarrow (x^3+x^2+3x+4) +(x^4+5x+6)\\\\=x^4+x^3+x^2+8x+10\\\\2.\rightarrow (x^3+x^2+3x+4) -(x^4+5x+6)\\\\=-x^4+x^3+x^2-2x-2\\\\3.\rightarrow (x+2)* x^2\\\\=x^3+2x^2\\\\4.\rightarrow (x^3+2x^2)/(x)\\\\\rightarrow x^2+2x`

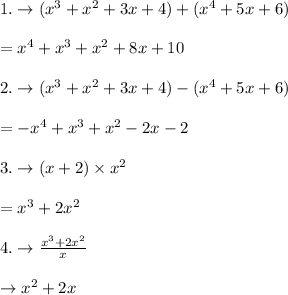
Real world Situation

There is a large enclosed room .We want to place bulbs in ceiling.To do that,we draw few straight lines that is Linear polynomial columnwise and then we have drawn Linear polynomial Row wise.The point of intersection of these lines gives the points where the bulbs should be fixed.Now ,if we join these points where the bulb is placed we will get a new polynomial.