Answer:
The angle between
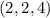 and
and
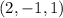 is 60º.
is 60º.
Explanation:
From linear algebra, we can determine the angle between both vectors by definition of dot point:
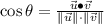 (1)
(1)
Where:
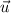 ,
,
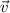 - Vectors.
- Vectors.
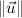 ,
,
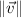 - Norms of vectors.
- Norms of vectors.
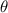 - Angle between vectors, measured in sexagesimal degrees.
- Angle between vectors, measured in sexagesimal degrees.
If we know that
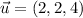 and
and
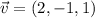 , then angle between vectors is:
, then angle between vectors is:
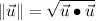 (2)
(2)
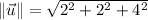
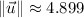
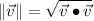 (3)
(3)
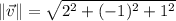
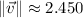
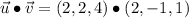
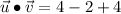
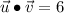
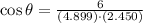
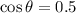
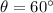
The angle between
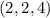 and
and
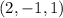 is 60º.
is 60º.