Question

A clown is juggling at a circus. The path of the ball is given by the parametric equations x=2cos t+2 and y=3sin t+3. In what direction is the ball moving?

-up and to the right
-counterclockwise
-down and to the right
-clockwise

Answer 1

1. B. Counterclockwise

2. C. (30,401)

3. A. t=2(x-3)

4. C. She should have taken both the positive and negative square root

5. C. y=x^2+8x-25/8

6. D. Hyperbola

7. A. Graph A

Answer 2

We need to find the direction the ball is moving, so wee have this parametric equation, namely:

`\left \{ {{x=2cost+2} \atop {y=3sint+3}} \right.`

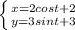
Note that this parametric equation is an ellipse. The graph of this equation is given in figure below. So, we well substitute some values of t in the equation:

If t = 0
x = 4 and y = 3
P0(4, 3)

if t = 1
x = 3.08 and y = 5.52
P1(3.08, 5.52)

if t = 2
x = 1.16 and y = 5.72
P2(1.16, 5.72)

Finally, as shown in the figure, the answer is B. counterclockwise. Notice the trajectory that follows P0, P1 and P2.