Question

Two cubes have surface areas of 72 square feet and 98 square feet. what is the ratio of the volume of the small cube to the volume of the large cube?

Answer 1

Let's denote the sides of the small and bigger cubes a and b respectively. Then, we can write that 6
`a^(2)`=72, a=
`2√(3)` and 6
`b^(2)=98, b=[tex] \frac{7}{sqrt{3}}`. The volume of the smaller cube is
`2 sqrt{3} ^(3)` =
`24 sqrt{3}`. The volume of the bigger cube is
`\frac{7}{sqrt{3}}^(3)` =
`\frac{343}{3sqrt{3}}{`. We have to find
= 216/343

Answer 2

Ratio of the volumes of the cubes = 216 : 343

Explanation:

Since surface area of a cube is represented as 6a² where a is the side of a cube.

Let a is one side of large cube and b is the side of smaller one.

Ratio of their surface area =
`(6a^(2) )/(6b^(2))=(72)/(98)`

`((a)/(b))^(2)=(36)/(49)`

`(a)/(b)=\sqrt{(36)/(49)}`

`(a)/(b)=(6)/(7)`

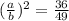
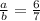
Now ratio of the volumes =
`(a^(3) )/(b^(3))=((1)/(b))^(3)`

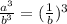
Ratio =
`((6)/(7))^(3)=(216)/(343)`

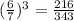
Therefore, ratio of the volumes of the cubes = 216 : 343