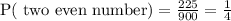Question

A bag contains 30 lottery balls numbered 1-30 a ball is selected replaced then another is drawn find each probability

p ( and even,then odd )
p ( 7, then a number greater than 16)
p ( a multiple of 5, then a prime number )
p ( two even number )

Answer 1

Given : A bag contains 30 lottery balls numbered 1-30 a ball is selected replaced then another is drawn.

To find : Each probability

1) p ( and even,then odd )

2) p ( 7, then a number greater than 16)

3) p ( a multiple of 5, then a prime number )

4) p ( two even number )

Solution :

`\text{Probability}=\frac{\text{Favorable outcome}}{\text{Total number of outcome}}`

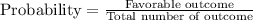
1) There are 15 even numbers and 15 odd numbers.

Probability of getting even first then odd is

`\text{P(even,then odd)}=(15)/(30)*(15)/(30)`

`\text{P(even,then odd)}=(225)/(900)=(1)/(4)`

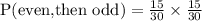
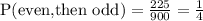
2) Number greater than 16 out of 30 are 14.

Probability of getting 7 first then a number greater than 16 is

`\text{P(7, then a number greater than 16)}=(1)/(30)*(14)/(30)`

`\text{P(7, then a number greater than 16)}=(14)/(900)=(7)/(450)`

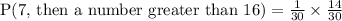
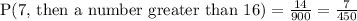
3) Multiple of 5 - 5,10,15,20,25,30=6

Prime numbers - 2,3,7,9,11,13,17,19,23,29=10

Probability of getting a multiple of 5, then a prime number is

`\text{P(a multiple of 5, then a prime number )}=(6)/(30)*(10)/(30)`

`\text{P(a multiple of 5, then a prime number )}=(60)/(900)=(1)/(15)`

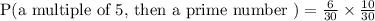
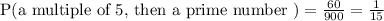
4) There are 15 even numbers.

Probability of getting two even number is

`\text{P( two even number)}=(15)/(30)*(15)/(30)`

`\text{P( two even number)}=(225)/(900)=(1)/(4)`