Question

A missile is launched upward with a speed that is half the escape speed. What height (in radii of Earth) will it reach?

Answer 1

The height (h) will be:
`(3)/(4)R =h`

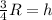
Step-by-step explanation:

The scape speed equation is given by:

`v_(scape)=\sqrt{(2GM)/(R)}`

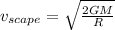
Now, the speed of the missile is

`v_(missile)=(1)/(2)v_(scape)`

`v_(scape)=(1)/(2)\sqrt{(2GM)/(R)}`

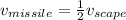
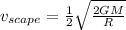
Using the conservation of energy, we can find the maximu height of the missile.

`E_(i)=E_(f)`

`(1)/(2)mv_(scape)^(2)-mgR =-mgh`

`(1)/(2)(2GM)/(4R)-gR =-gh`

`(GM)/(4R)-gR =gh`

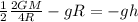
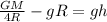
Let's recall that g = GM/R², using the equivalence principle. When R is the radius of the earth and M is the mass of the earth.

`(1)/(4)gR-gR =-gh`

`(1)/(4)R-R =-h`

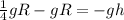
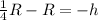
Therefore the height (h) will be:

`(3)/(4)R =h`

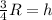
I hope it helps you!