The correct answer is A. NGNGATo find a sequence is arithmetic, we are going to find its common difference:

where

is the common difference

is the current term in the sequence
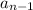
is the previous term in the sequence
To find if a sequence is geometric, we are going to find its common ratio:
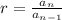
where

is the common ratio

is the current term in the sequence
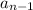
is the previous term in the sequence
1) 3,4,6,10,18
For
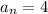
and
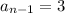
:

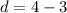

For
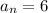
and
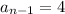
:
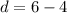
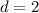
For
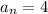
and
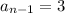
:
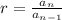
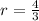
For
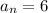
and
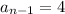
:
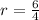
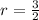 We can conclude that the sequence is neither arithmetic nor geometric.
We can conclude that the sequence is neither arithmetic nor geometric.
2) 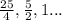
For

and
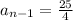
:

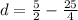

For

and
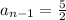
:
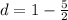
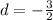
For

and
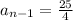
:
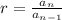

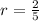
For

and
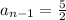
:
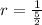
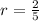 We have a common ratio, we can conclude that the sequence is geometric.
We have a common ratio, we can conclude that the sequence is geometric.
3) 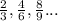
For
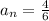
and

:

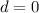
For
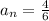
and

:
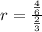
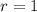
For
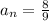
and

:
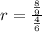
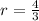 We can conclude that the sequence is neither arithmetic nor geometric.
We can conclude that the sequence is neither arithmetic nor geometric.
4) 3,15,75...
For
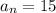
and
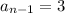
:

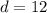
For

and
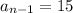
:
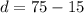
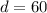
For
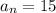
and
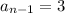
:

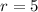
For

and
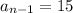
:
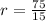
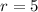 We have a common ratio, we can conclude that the sequence is geometric.
We have a common ratio, we can conclude that the sequence is geometric.
5) 5,-11,-27
For
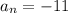
and
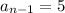
:
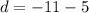
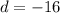
For
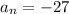
and
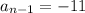
:
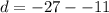

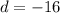 We have a common difference, we can conclude that the sequence is arithmetic.
We have a common difference, we can conclude that the sequence is arithmetic.