Question

Suppose there are 50 possible dancers. How many trios may be formed, assuming the order within a trio does not matter

Answer 1

19600 trios may be formed.

Explanation:

Since the order of the trios do not matter, we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this question:

Groups of three(Trios) from a set of 50. So

`C_(50,3) = (50!)/(3!(50-3)!) = 19600`

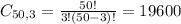
19600 trios may be formed.