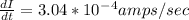Question

where V is the voltage in volts, I is the current in amperes, and R is the resistance in ohms. Assume that, as the battery wears out, the voltage decreases at 0.03 volts per second and, as the resistor heats up, the resistance is increasing at 0.02 ohms per second. When the resistance is 100 ohms and the current is 0.02 amperes, at what rate is the current changing

Answer 1

`(dI)/(dt) =-3.04*10^-^4amps/sec`

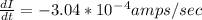
Step-by-step explanation:

From the question we are told that

Voltage change
`(dv)/(dt)=-0.03volts/sec`

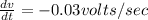
Resistance change
`(dR)/(dt)=0.02ohms/sec`

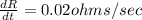
Resistance
`R=100`

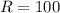
Current
`I=0.02`

Generally the equation for ohms law is mathematically represented as

`V=IR`

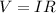
Therefore

`(dv)/(dt) =R(dI)/(dt) +I(dR)/(dt)`

`(dv)/(dt) =R(dI)/(dt) +I(dR)/(dt)`

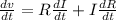
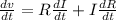
Resolving the Rate of current changing
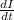`(dI)/(dt)` as subject of formula

`(dv)/(dt) =R(dI)/(dt) +I(dR)/(dt)`

`R(dI)/(dt) =(dv)/(dt) -I(dR)/(dt)`

`(dI)/(dt) =(1)/(R) ((dv)/(dt) -I(dR)/(dt))`

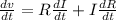
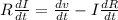
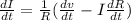
Therefore

`(dI)/(dt) =((-0.03) -(0.02)(0.02))/(100)`

`(dI)/(dt) =-3.04*10^-^4amps/sec`

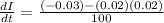
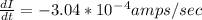
Therefore the current decreases at a rate

`(dI)/(dt) =3.04*10^-^4amps/sec`