2 Answers

Angel Yan · Answer 1 · 2019-12-09T19:51:12+0000

We have been given a system of nonlinear equations.

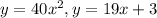
$\\y=40x^(2),y=19x+3$

In order to solve this system we can first equate the two equations in order to get a quadratic in x.

$\\40x^(2)=19x+3$

Our next step is to bring all the terms on one side.

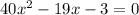
$\\40x^(2)-19x-3=0$

Now we have to solve this equation. We can solve it by factoring using the splitting middle term method.

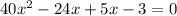
$\\40x^(2)-24x+5x-3=0$

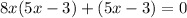
$\\8x(5x-3)+(5x-3)=0$

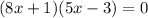
$\\(8x+1)(5x-3)=0$

Upon setting each of these factors equal to zero using zero product property we get

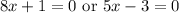
$\\8x+1=0 \text{ or } 5x-3 = 0$

Upon solving both these equations we get

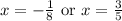
$\\x=-(1)/(8) \text{ or } x=(3)/(5)$

Now we can substitute these values of x in the equation

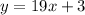
y=19x+3

We get

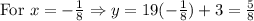
$\text{For }x=- (1)/(8) \Rightarrow y=19(- (1)/(8))+3= (5)/(8)\\$

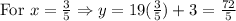
$\text{For }x= (3)/(5)\Rightarrow y=19( (3)/(5))+3= (72)/(5)\\$

Therefore, our final set of solutions are

$(x,y)=(- (1)/(8),(5)/(8)) \text{ and } ( (3)/(5), (72)/(5))$

Please log in or register to add a comment.