Question

Five times of a positive integer is less than twice its square by 3.
Find the integer.

Answer 1

The positive integer is 3.

Explanation:

Let 'x' be the integer

Given that five times of a positive integer is less than twice its square by 3.

so

5 times of x =
`5x`

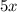
3 less than twice of the square of x =
`2x^(2) - 3`

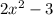
so the equation becomes

`5x = 2x^(2) - 3`

`2x^2-5x-3=0`

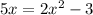
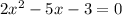
Factorise

`\left(2x+1\right)\left(x-3\right)=0`

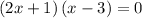
Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

`2x+1=0\quad \mathrm{or}\quad \:x-3=0`

solving

`2x+1=0`

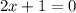
Subtract 1 from both sides

`2x+1-1=0-1`

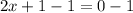
Simplify

`2x=-1`

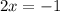
Divide both sides by 2

`(2x)/(2)=(-1)/(2)`

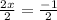
Simplify

`x=-(1)/(2)`

Also solving

`x-3=0`

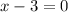
Add 3 to both sides

`x-3+3=0+3`

simplify

`x=3`

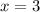
Thus, we got integers:

x = 3 or x = -1/2

• As x can not be a negative integer according to the question.

Therefore, the positive integer is 3.