Question

Penn stacks all of his snowballs in a square pyramid. The number of snowballs, P(n), in n layers of the square pyramid is given by P(n) = P(n-1) + n^2 Which could not be the number of snowballs Penn has? 5, 30, 25, 14

Answer 1

Naturally, a pyramid of zero layers doesn't need any snowballs, so P(0) = 0. Then using the given recurrence, we find

P(1) = 1

P(2) = 1 + 4 = 5

P(3) = 1 + 4 + 9 = 14

P(4) = 1 + 4 + 9 + 16 = 30

and so on; luckily, three of these are listed among the answer choices, which leaves 25 as an insufficient number of snowballs to make such a pyramid.

More generally, we would end up with

`P(n) = 1^2 + 2^2 + 3^2 + \cdots + n^2 = \displaystyle \sum_(k=1)^n k^2 = \frac{n(n+1)(2n+1)}6`

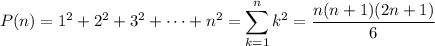
Then given some number of snowballs S, you could try to solve for n such that

S = n (n + 1) (2n + 1)/6

and any S that makes n a non-integer would be the answer.